Dynamic Thermal Rating in Diverse Climatic Conditions: Uncertainty Analysis and Fuzzy Logic Approach

Abstract

In recent times, there has been a significant rise in the need for electricity, a trend expected to continue. This surge in demand has resulted in transmission lines operating at much higher capacities, which in turn exposes them to increased thermal and mechanical stress, ultimately impacting the reliability of the transmission network. In this paper presents a comprehensive analysis of the static thermal rating (STR) and dynamic thermal rating (DTR) of power lines across varied climatic conditions. The study encompasses a thorough investigation into the thermal behavior of power lines during both summer and winter seasons over a 24-hour period. Through rigorous computational simulations and empirical data collection, the STR and DTR profiles are determined to assess the real-time capacity of power lines under changing environmental conditions. Furthermore, the research introduces a novel approach utilizing fuzzy logic to model the dynamic thermal rating (FDTR) based on the IEEE 738 standard, in regions characterized by diverse climatic patterns. By integrating fuzzy logic with meteorological data, the FDTR model offers enhanced accuracy in predicting the thermal performance of power lines, considering factors such as ambient temperature, wind speed, and solar radiation. The proposed methodology aims to provide utilities and grid operators with a reliable tool for optimizing power transmission capacity, mitigating the risk of overheating, and ensuring grid reliability in regions with complex and fluctuating weather conditions. This study contributes to the advancement of smart grid technology and facilitates efficient energy management in diverse climate zones

Introduction

I. INTRODUCTION

As electricity demand outpaces transmission capacity growth, the evolution of electric power networks becomes imperative to meet the rising energy needs sustainably. Integrating renewable energy sources into existing infrastructures without sacrificing overhead conductors offers a promising solution. To address this challenge, power utilities must embrace innovative and flexible network enhancement strategies [1]. These approaches aim to enhance power transfer capabilities while minimizing the need for significant investments in new assets. The ultimate goal is to transition traditional power networks into adaptable smart systems capable of accommodating diverse and expanding energy demands efficiently.

Electric power transmission systems rely on two key methods to determine the current-carrying capacity of transmission lines: Static Thermal Rating (STR) and Dynamic Thermal Rating (DTR). While STR establishes a fixed maximum capacity based on limited environmental assumptions, DTR revolutionizes this approach. By integrating real-time weather data and advanced algorithms, DTR forecasts the actual capacity of transmission lines, enhancing operational efficiency and optimizing power system management [2]. This dynamic approach not only increases line capacity but also enables proactive planning and control, ushering in a new era of reliability and sustainability in energy transmission.

Transitioning from fixed load demand to dynamic thermal rating (DTR) coupled with demand-side management enhances the responsiveness and safety of power systems [3]. By enabling active control over flexible resources on the load side, DTR ensures the safe operation of power equipment. Moreover, the integration of storage technologies and management systems further augment’s reliability and utilization of electric power [4]. Research indicates that DTR plays a crucial role in facilitating the integration of renewable energy sources, particularly wind turbines, into the grid [5]. This integration not only satisfies additional load points but also maintains financial viability during emergencies, thereby reducing the necessity for additional transmission assets. Additionally, compared to constructing new lines or upgrading major infrastructure, implementing DTR proves to be a cost-effective solution. Therefore, the shift from static dynamic rating (STR) to DTR offers numerous benefits in terms of efficiency, reliability, and cost-effectiveness [6].

Enhancing the load-carrying capacity of overhead transmission lines (OHL) while managing conductor temperatures is imperative for ensuring the reliability and economic viability of power systems. The dynamic line rating approach offers practical solutions for meeting increasing load demands; however, it also poses challenges due to the potential for excessive conductor temperatures, which can accelerate degradation mechanisms such as annealing and aging. The rate of component aging directly correlates with the magnitude and duration of thermal overload, further underscoring the importance of addressing conductor thermal behavior. As highlighted in previous studies [7], the progressive deterioration of electric components adversely impacts system reliability and economics. Therefore, ongoing research efforts are crucial for improving OHL load capacity and mitigating thermal stress and aging effects on conductors [8]. Various studies have been conducted to address these challenges and enhance the performance or line rating of transmission systems [9].

Moreover, the assessment of Dynamic Thermal Ratings (DTR) encounters significant uncertainty stemming from the sparse distribution of sample stations along transmission lines, inherent measurement inaccuracies, and unpredictable weather fluctuations. Scholars have extensively deliberated on the reliability and safety concerns surrounding monitoring stations and the overarching communication infrastructure. In order to attain a more precise estimation of line ratings and conductor temperatures, it is imperative to incorporate uncertainties into the computations. While probabilistic tools exhibit proficiency in modeling parameter uncertainties, their applicability is somewhat constrained by the necessity of specifying standard probability distributions for uncertain parameters. Consequently, the application of fuzzy sets has emerged as the preferred approach for modeling the uncertainty inherent in meteorological data. Furthermore, fuzzy reasoning has demonstrated efficacy in optimizing the control of transmission line overloading, as evidenced by prior research. Additionally, a method based on fuzzy logic has been introduced for computing transmission line ampacity, further underscoring the versatility and effectiveness of fuzzy-based approaches in addressing the challenges associated with transmission line management [10].

Researchers have frequently employed the heat balance equation of overhead line conductors to examine their thermal characteristics. By utilizing this equation, studies have aimed to estimate conductor temperatures under varying conditions. Real-time monitoring of meteorological conditions facilitates the application of these equations to calculate the dynamic thermal rating of the line, enabling a deeper understanding of its thermal behavior [11].

This research paper employs static thermal rating, which involves determining the maximum permissible current a conductor can carry under steady-state conditions and Dynamic thermal rating is investigated to assess the conductor's capability to handle varying load conditions over time. To address uncertainties associated with dynamic thermal rating, fuzzy dynamic thermal rating techniques are utilized, allowing for a more nuanced understanding of thermal performance, especially in diverse climatic regions. The utilization of the Fuzzy Dynamic Thermal Rating (FDTR) system was motivated by its capacity to defer and circumvent significant line capital outlays [12]. Its cost efficiency and expedited deployment compared favorably with conventional line augmentation methodologies. Concurrently, FDTR calculations incorporated historical weather patterns, thereby enhancing accuracy. Numerical simulations were executed using datasets sourced from authentic repositories for comprehensive analysis.

II. METHODOLOGY

A. Theory of Dynamic Thermal Rating System

The steady-state dynamic thermal rating of exposed overhead conductors is determined according to the IEEE 738 standard [11], which considers meteorological factors. Key variables influencing DTR include solar heat absorption, convective heat dissipation to the surrounding air, radiative heat exchange with the environment, and the current flowing through the conductor. When environmental conditions are stable, the conductor's current-carrying capacity is dictated by the equilibrium between heat gained and lost. This is expressed through the steady-state heat balance equation for the conductor.

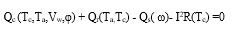
Where, Qc stands for the loss of heat via convection, while Qr indicates heat loss through radiation. Conversely, Qs represents the gain of heat through radiation, and I2R(Tc) illustrates the heat generated by the flow of current within a conductor, with I representing the maximum permissible current, equal to the line rating. These thermal factors are contingent upon several meteorological variables, such as ambient temperature (Ta), solar radiation angle (ω), wind speed (Vw), and incident wind angle (φ) relative to the line. Additionally, the temperature of the conductor (Tc) and its resistance (R), which varies based on temperature, play pivotal roles in determining these thermal influences.

Thus, the maximum current capacity permissible for the conductor amidst prevailing weather conditions can be determined from the Equation (1). The acceptable temperature range for the conductor may vary between steady-state and dynamic conditions. Consequently, different permissible currents are derived for each condition.

B. Assessment of Heat Loss Rate

The convective heat loss rate of a conductor depends on various factors such as wind speed and direction, air and conductor temperature, dynamic viscosity, density of the air, and the conductor's diameter. These factors influence the estimation of the maximum heat loss rate applicable in different wind conditions [11]. Additionally, the radiated heat loss rate is determined by the conductor's diameter, ambient and conductor temperatures, and a parameter denoted as α. The darkness of the conductor's surface affects its ability to absorb heat, thus impacting the radiated heat loss. The parameter α typically falls within the range of 0.23 to 0.91, depending on the condition of the conductor surface.

C. Assessment of solar heat Gain Rate

Solar heat intensity experiences variations across seasons and different times of the day, making its energy dependent on factors such as the projected area of the conductor (Ar), latitude (Lat), and solar absorptivity (α). It's noteworthy that α is considered equivalent to emissivity (ε). The latitude (Lat) typically spans from -90 to +90 degrees, while solar declination ranges from 0 to 90 degrees. Key determinants affecting heat flux density include solar altitude (Hc), hourly angle (ω), and atmospheric clarity, as outlined in reference [11].

When accounting for uncertainty, it’s common to work with ranges of values, known as fuzzy numbers. This fuzzy numbers allow for a more nuanced understanding of the variable involved. In [10] a more detailed explanation of the equations involved.

III. EXPERIMENTAL RESULTS AND DISCUSSION

To demonstrate the practical use of thermal rating forecasting, let’s examine a 100km segment of a power transmission line in Assam, India, which experiences varied climatic conditions. The conductor considered is a Drake ACSR conductor, and parameter such as windspeed, wind angle, ambient temperature, solar angle are selected based on climatic conditions of the Assam region. The maximum line loading is set at 3000A, with an additional transmission capacity reserve of 10% [13].

In Assam, transmission lines equipped with ACSR conductors are designed to support a maximum static rating of 992A each conductor. This rating is established through calculations that anticipate the conductor’s temperature reaching 75 oC under predefined circumstances. These circumstances encompass an assumed wind speed of 3.6m/s, an ambient temperature of 27 oC, and a solar radiation intensity of 1024 W/m2[14] .

Fig.1 displays the comparison of dynamic thermal ratings for summer and winter, highlighting their variance from static thermal rating. Also it indicates that the Dynamic thermal rating for winter season is higher compared to that for summer. To address the uncertainty surrounding dynamic thermal rating, fuzzy dynamic thermal rating is utilized. Fig.2 illustrates the comparison between fuzzy dynamic thermal rating, real-time dynamic thermal rating, and static thermal rating during the winter season. Fig.3 depicts a comparison between fuzzy dynamic thermal rating, real-time dynamic thermal rating, and static thermal rating during the summer season. Fig.4 shows the variation of fuzzy dynamic thermal rating throughout the winter and summer seasons.

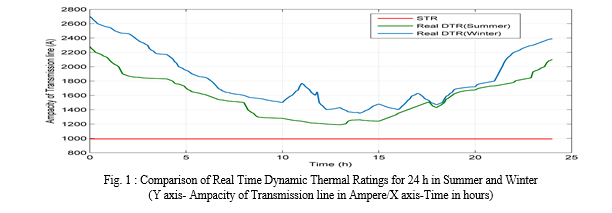
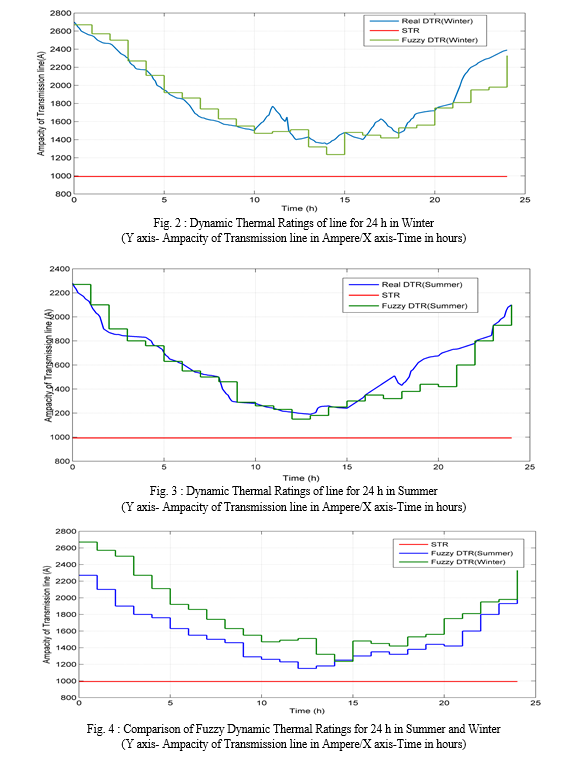
In Fig.1, the dynamic thermal ratings gradually decrease up to 10 hours in both summer and winter seasons. However, at 11.5 hours, there is a significant contrast between winter and summer dynamic thermal ratings, with winter’s Real DTR at 1765A and summer’s at 1238 A. After 16 hours, the dynamic thermal ratings start increasing. The contrast between winter and summer dynamic thermal ratings at 11 hours could be due to variations in temperature and load conditions. Winter temperatures are typically lower, resulting in higher dynamic thermal ratings due to improved cooling efficiency. Additionally, load patterns may differ between seasons, affecting the overall stress on the transmission lines. In Fig.2, for the winter season, at 14 hours, the fuzzy dynamic thermal rating shows 1235A, while the real DTR is 1350A. This change may be occurring due to various factors such as fluctuating environmental conditions, changes in power consumption patterns or adjustments in the fuzzy logic control system. In Fig.3, the lowest dynamic thermal rating reaches 1190A at 13 hours. Fig.4, the curves of fuzzy dynamic thermal rating converge at 14 hours in both winter and summer seasons. This may occur due to consistent environmental conditions, balanced power demand, or adjustments made in the fuzzy logic control system to optimize thermal performance.

Conclusion

This research paper comprehensively evaluated the steady-state thermal rating and dynamic thermal rating over a 24-hour period, considering both summer and winter seasons. By comparing these ratings across seasons, the study provided valuable insights into the thermal behavior of the system under diverse climatic conditions, such as those found in regions like Assam. For instance, at 15 hours, the real time dynamic thermal rating is 1480 A during winter season and 1240 A during the summer season. Furthermore, recognizing the inherent uncertainties associated with dynamic thermal rating, the research proposed a novel approach: fuzzy dynamic thermal rating. This methodology offers a robust framework to address uncertainties, accommodating the variability of climatic conditions and their impact on thermal ratings. By integrating fuzzy logic principles, the fuzzy dynamic thermal rating accounts for the complex interplay of factors influencing thermal performance, providing a more nuanced understanding of system behavior. The findings of this study contribute to the advancement of thermal rating methodologies, particularly in regions with diverse and challenging climatic environments like Assam, ultimately enhancing the reliability and efficiency of power infrastructure in such areas. The future scope could involves integrating renewable energy sources, utilizing smart grid technologies, implementing machine learning algorithms for predictive analysis, developing optimization techniques, conducting field trials, examining policy implications, exploring resilience strategies, and assessing environmental impacts. These areas collectively aim to advance the understanding and implementation of dynamic thermal ratings, especially in regions with diverse climatic conditions

References

[1] P. Patowary, Dynamic thermal rating and allowable operating time under transient conditions, in 2014 Eighteenth National Power Systems Conference (NPSC) IEEE,2014, pp.1-6. [2] O. A. Lawal , J. The, Dynamic Thermal Rating Forecasting Methods: A Systematic Survey, in IEEE Access, vol. 10,2022, pp. 65193-65205 [3] Lai, C.M., Teh, J., Comprehensive Review of the Dynamic Thermal Rating System for Sustainable Electrical Power Systems. Energy Rep. 2022, 8, 3263–3288. [4] Khoo, W.C ,Teh, J., Lai, C.M. Demand Response and Dynamic Line Ratings for Optimum Power Network Reliability and Ageing. [5] IEEE Access 2020, 8, 175319–175328. [6] Teh. J., Cotton, I. Reliability Impact of Dynamic Thermal Rating System in Wind Power Integrated Network. IEEE Trans. Reliab.2016, 65, 1081–1089. [7] Teh, J., Lai, C.M., Muhamad, N.A., Ooi, C.A., Cheng, Y.H., Zainuri, M.A.A.M., Ishak, M.K. Prospects of Using the Dynamic Thermal Rating System for Reliable Electrical Networks: A Review. IEEE Access 2018, 6, 26765–26778. [8] Musilek, P., Heckenbergerova, J., Bhuiyan, M.M.I. Spatial Analysis of Thermal Aging of Overhead Transmission Conductors. IEEE Trans. Power Deliv. 2012, 27, 1196–1204 [9] Erdinç, F.G., Erdinç, O., Yumurtac?, R., Catalão, J.P.S. A Comprehensive Overview of Dynamic Line Rating Combined with Other Flexibility Options from an Operational Point of View. Energies 2020, 13, 6563. [10] Zainuddin, N.M.; Rahman, M.S.A., Kadir, M.Z.A.A.,Ali, N.H.N., Ali, Z., Osman, M.; Mansor, M., Ariffin, A.M., Nor, S.F.M., Nasir, N.A.F.M. Review of Thermal Stress and Condition Monitoring Technologies for Overhead Transmission Lines: Issues and Challenges. IEEE Access 2020, 8, 120053–120081 [11] Shaker, H., Fotuhi-Firuzabad, M., Aminifar, F. Fuzzy Dynamic Thermal Rating of Transmission Lines. IEEE Trans. Power Deliv.2012, 27, 1885–1892. [12] IEEE Std 738TM-2012; IEEE Standard for Calculating the Current-Temperature Relationship of Bare Overhead Conductors .Committee of the IEEE Power; IEEE Power and Energy Society: New York, NY, USA, 2012. [13] Bell, K.R.W., Daniels, A.R., Dunn, R.W. Alleviation of Transmission System Overloads Using Fuzzy Reasoning. Fuzzy Sets Syst.1999, 102, 41–52. [14] Larruskain, D.M.; Zamora, I.; Abarrategui, O.; Iraolagoitia, A.; Gutiérrez, M.D.; Loroño, E.; de la Bodega, F. Power Transmission Capacity Upgrade of Overhead Lines. Renew. Energy Power Qual. J. 2006, 1, 221–227. [15] Analysis and Overcurrent Relay Adaptation Strategies for Mitigation - Lakhyahira Baishya, Purobi Patowary, Dhritika Saikia - IJFMR Volume 6, Issue 3, May-June 2024. DOI 10.36948/ijfmr.2024.v06i03.19641

Copyright

Copyright © 2024 Lakhyahira Baishya , Purobi Patowary. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.